Rumus Menghitung Lendutan Kantilever – Pada kesempatan kali ini kami akan membahas mengenai cara menghitung lendutan pada balok sederhana. Sebelumnya perlu diketahui bahwa selain momen dan geser yang harus diperhitungkan pada balok sederhana akibat sebuah beban, lendutan yang terjadi pada balok tersebut juga menjadi hal yang penting.
Dalam sebuah perencanaan, seperti pembangunan jembatan maupun bangunan gedung maka pada masing-masing baloknya tentu mempunyai syarat-syarat atau batas-batas lendutan yang dimana sudah diatur dengan standar yang ditentukan oleh beberapa ahli.
Lalu mengapa lendutan umumnya baru dibahas setelah membahas mengenai perhitungan berbagai gaya dalam baik itu momen ataupun gaya geser? Hal ini karena memang tahapan langkah untuk dapat mengetahui lendutan sebuah balok harus diketahui momen yang terjadi pada balok tersebut akibat beban yang bekerja.
Baca juga: Pengertian Dan Perhitungan Beton Prategang
Cara Menghitung Lendutan pada Balok dengan Beban Terpusat
Selain harus mengetahui momen yang terjadi, untuk menghitung lendutan pada balok juga harus mengetahui Modulus Elastisitas (E) dan Inesia (Ix) penampang balok itu sendiri. Sedangkan cara yang bisa dilakukan untuk mendapatkan modulus elasitisas dan Inersia penampang bisa dibilang cukup mudah.
Modulus elasitas penampang balok sebenarnya ditentukan oleh bahan yang digunakan. Jika misalnya menggunakan struktur baja, maka untuk modulus elasitasnya adalah sebesar 200.000 Mpa. Sedangkan jika menggunakan struktur beton maka untuk modulus eleasitasnya bisa dicari dengan menggunakan rumus sebagai berikut, 4700 x akar (fc’). Dalam hal ini hasilnya adalah menggunakan satuan MPa.
Sementara itu, untuk mendapatkan data inersia penampang maka harus mengetahui ukuran detail penampang terlebih dahulu. Kemudian perlu dilakukan analisa secara manual atau bisa juga menggunakan software khusus. Untuk lebih jelasnya, silahkan Anda perhatikan contoh soal berikut ini.
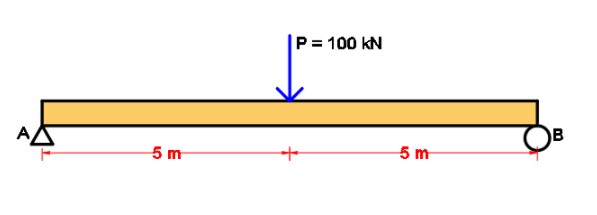
- Carilah Nilai Reaksi yang Terjadi Pada Model Pembebanan.
Jika beban terpusat di tengah bentang seperti yang bisa Anda lihat pada contoh tersebut maka reaksi yang akan terjadi pada kedua tumpuan akan sama, yakni sebesar RA = RB = P/2 = 100/2 = 50 kN.
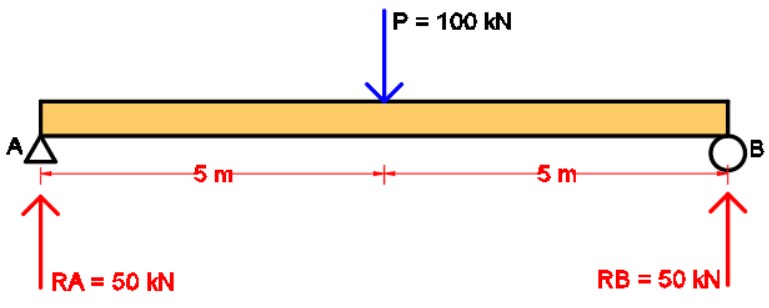
- Hitunglah Momen Maksimum yang Terjadi Akibat Pembebanan.
Beban terpusat di tengah bentang pada contoh tersebut mempunyai momen maksimum yang juga terpusat di tengah bentang. Dengan reaksi yang mencapai RA = 50 kN maka untuk momen maksimum yang bisa terjadi adalah Mmax = RA x 5 = 50 x 5 = 250 kNm.
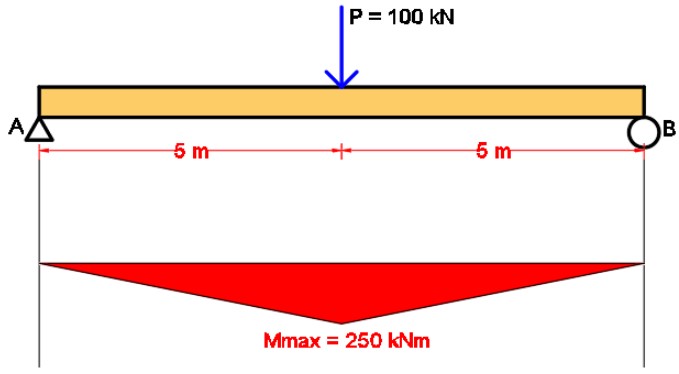
- Momen yang Terjadi Akan Dijadikan Sebagai Beban pada Struktur yang Sama.
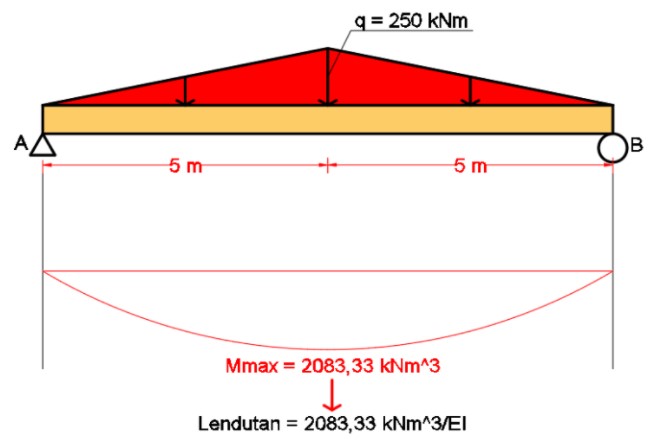
Seperti yang bisa Anda lihat pada gambar berikut ini. Momen yang sebelumnya sudah dihitung bisa dijadikan sebagai beban untuk struktur yang sama seperti contoh soal sebelumnya. Mmax = 250 kNm akan berubah menjadi q = 250 kNm. Sehingga untuk bebannya adalah berupa segitiga.
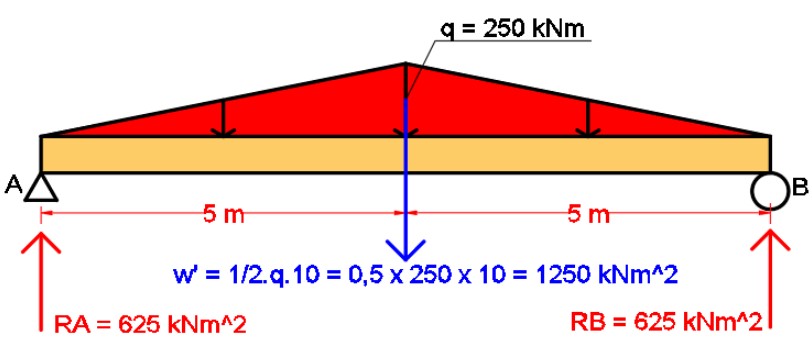
w = 1/2qL = 1/2 x 250 x 10 = 1250 kNm^2
RA = RB = 1/2w = 1/2 x 1250 = 625 kNm^2
Selanjutnya adalah menghitung kembali reaksi yang terjadi akibat pembebanan tersebut. Sehingga diperoleh:
- Hitunglah Kembali Momen Maksimum Akibat Pembebanan Tersebut.
Berikut ini kami akan memberikan contoh permisalan q’ dan w’. Untuk q’ disini diperoleh sebesar 50x sedangkan w’ sebesar 25x^2. Dengan demikian, maka Mx = RA.x – w’.1/3x = 625x – (25/3x^3).
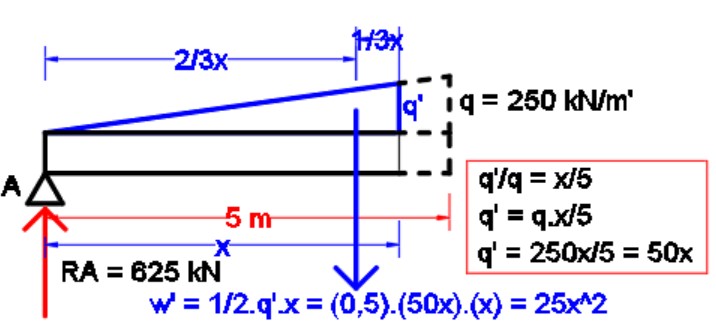
Momen maksimum sudah pasti berada di tengah bentang (x = 5mm) karena beban yang simetris. Sehingga:
Mmax = 2083,33 kNm^3

Momen maksimum di atas akan menjadi dasar lendutan pada contoh soal yang pertama. Adapun lendutannya adalah sebagai berikut:
Lendutan maksimum (pada x = 5m) = (2083,33 kNm^3)/EI
Keterangan:
E adalah Modulus Elastisitas (MPa)
I adalah Momen Inersia Penampang (cm4)
Catatan: Supaya mendapatkan hasil yang benar maka untuk satuan di atas harus disesuaikan terlebih dahulu. Sebagai contoh, momen Inersia menjadi mm4 dan lendutan dalam (… Nmm^3/EI).
Cara Menghitung Lendutan pada Balok dengan Beban Merata
Selanjutnya kami akan menjelaskan cara menghitung lendutan yang terjadi pada balok sederhana dengan beban merata di semua bentangnya. Berikut ini kami akan memberikan contoh soalnya.
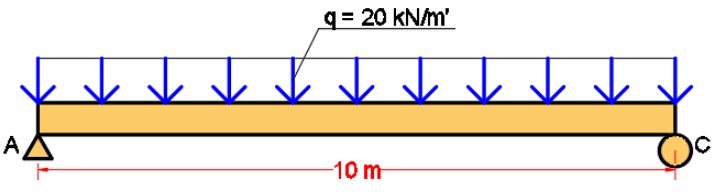
Balok sederhana yang memiliki bentang 10 meter dibebani beban terbagi rata sepanjang balok sebesar q = 20 kN/m’. Hitunglah lendutan yang terjadi jika Modulus Elastisitas (E) diketahui sebesar 200000 MPa dan Momen Inersia Penampang (Ix) sebesar 100000 cm^4.





